Altın Oran’ın Gizemi
PROF. DR. SALİM YÜCE
YILDIZ TEKNİK ÜNİVERSİTESİ MATEMATİK BÖLÜMÜ ÖĞRETİM ÜYESİ
21. YÜZYILDA Fİ, ZAMAN VE KUANTUM FİZİĞİ DE DÂHİL OLMAK ÜZERE ÇOK ÇEŞİTLİ ÇALIŞMA ALANLARINDA YENİDEN DOĞUYOR.
Yaratıcının doğayı keşfetmemiz, anlamamız ve yorumlamamız için kodladığı dillerden birinin adıdır matematik. Bu dilin görüntüleme boyutu da geometridir. Birbirini destekleyen iki kavram olarak matematik ve evren birbirlerinin içinde gizlidir. Matematiğin içinde evren ve evrenin içinde matematik vardır. Doğayı seyretmeye başladığınız zaman evrenin içinde gizli olan matematiği keşfetmeye başlayabilirsiniz. Evrenin içinde gizli olan matematiğin kavramları olarak Fi(φ), Pi л(3,14…), e… sayılarını verebiliriz.
Fi sayısını sihirli yapan nedir? Antik Yunanlıların, Rönesans sanatçılarının, 17.
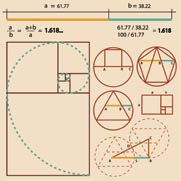 yüzyıl astronomu ve 21. yüzyıl romancısının hakkında çalışmalar yapacak kadar ilginç yapan nedir? Kısaca açıklamaya çalışayım: Yunanca Fi harfi ile temsil edilen bu ‘‘altın’’ sayı, 1.61803399…olup birçok isimle anılır. Altın Oran, Altın Sayı, Altın Ortalama, Altın Bölüm, İlahi Oran ve İlahi Bölüm olarak bilinir. Hayatın pek çok yönü için geçerli olan tasarım sabiti diyebileceğimiz Fi, alışılmadık bir şekilde sık sık ortaya çıkan
yüzyıl astronomu ve 21. yüzyıl romancısının hakkında çalışmalar yapacak kadar ilginç yapan nedir? Kısaca açıklamaya çalışayım: Yunanca Fi harfi ile temsil edilen bu ‘‘altın’’ sayı, 1.61803399…olup birçok isimle anılır. Altın Oran, Altın Sayı, Altın Ortalama, Altın Bölüm, İlahi Oran ve İlahi Bölüm olarak bilinir. Hayatın pek çok yönü için geçerli olan tasarım sabiti diyebileceğimiz Fi, alışılmadık bir şekilde sık sık ortaya çıkan
anlamları sayesinde bizleri çoğu zaman akademik değerin ötesinde manevi âlemine götürmüştür.
Bitkilerin yaprak dizilimi, insan bedeni ve bazı hayvanların vücut yapısı ile Altın Oran arasındaki bağlantılar incelendiğinde kâinatın muazzam dilinin izleri görülür. İzleri takip ettiğimizde yalnızca sıkıcı hesaplardan ibaret sanılan matematiğin evrende görünen yansımalarını fark etmeye başlarız. “Da Vinci Şifresi”nde de bir arsa öğesi olan
Fibonacci dizisi, Fi’yi matematiksel olarak elde etmenin bir diğer yolunu verir. Seri
oldukça basittir. 0 ve 1 ile başlayıp dizideki “her terim kendinden iki önceki terimin toplamı” ile elde edildiğini kabul edersek 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,… sayı dizisi elde edilir. Bu dizi Pascal üçgeninin köşegenlerinde de bulunur.
Bu diziyi
 oluşturan sayılar Fibonacci sayıları, Fn olarak bilinir. Fibonacci dizisinin Altın Oran ile olan ilişkisi, her sayının kendisinden öncekine bölünmesiyle bulunur. Dizide ne kadar ileri gidilirse sonuç Fi’ye o kadar yakın olur.
oluşturan sayılar Fibonacci sayıları, Fn olarak bilinir. Fibonacci dizisinin Altın Oran ile olan ilişkisi, her sayının kendisinden öncekine bölünmesiyle bulunur. Dizide ne kadar ileri gidilirse sonuç Fi’ye o kadar yakın olur.
ALTIN ORAN’IN GEOMETRİSİ
Fibonacci Dikdörtgenleri ve Fibonacci Sarmalları: Kenar uzunluğu 1 birim olan ve birbirine bitişik iki küçük kare ile başlayarak bu iki karenin her ikisinin üzerinde kenar uzunluğu 2 birim olan bir kare çizilirse bu üç kare ile kenar uzunlukları 2 ve 3 birim olan bir dikdörtgen bulunur. Bunların sağında 3 birimlik bir kare çizilirse her bir yeni karenin kenar uzunluğu önceki iki karenin kenar uzunluklarının toplamıdır. Hemen altlarında 5 birimlik bir kare daha çizilir ve devam edilirse karelerin kenar uzunlukları ve dikdörtgenlerin kenar uzunlukları ardışık Fibonacci sayıları 1, 1 ,2, 3, 5, 8, 13,… olur.
Böylece Fibonacci dikdörtgenleri elde edilmektedir.
Fibonacci dikdörtgenind
 e karelerin karşılıklı köşelerini Fibonacci sayılarıyla birleştiren yaylar çizilerek sarmal oluşturulabilir ve bu köşegenlerin kesişme noktası logaritmik sarmalın başlangıç noktasını verir.
e karelerin karşılıklı köşelerini Fibonacci sayılarıyla birleştiren yaylar çizilerek sarmal oluşturulabilir ve bu köşegenlerin kesişme noktası logaritmik sarmalın başlangıç noktasını verir.
DOĞA VE YAŞAM
Çam kozalağı oluşturan taneler alttaki sabit bir noktadan kozalağın tepesindeki noktaya doğru spiral şeklinde çıkarlar. Bu oluşan spirallerin eğriliğinin oranı; deniz kabuklarının yapılarında eğriliğin tanjantı; ayçiçeği tanelerinin sağdan sola ve soldan sağa sayılarının oranı; papatya çiçeğinin merkezinden sağa doğru gidenlerle sola doğru giden taneciklerin oranı (Bu sebepten çiçeklerin güneş ışığını en iyi şekilde almasını sağlamaktadır.); kar kristallerinin kısa uzantılarıyla, uzun uzantıları arasındaki oranı; tütün bitkisinin veya eğrelti otunun yapraklarının eğriliğinin oranı; geyik boynuzlarındaki çıkıntıların oranları; salyangozun kabuğu bir düzleme aktarılırsa bu düzlem bir dikdörtgen (altın dikdörtgen)
olup oluşan bu geometrik şeklin boyunun enine oranı; arının vücut kesitleri ile boyunun
oranları; yunus balığının başından kuyruğuna kadar uygun bölümler arasındaki oranları
doğanın sunduğu Altın Oran’a örnek olarak verebiliriz.

Gerçekten de içerisinde bulunduğumuz evrenin temelinde Altın Oran var mıdır yoksa çok eski çağlardan beri gelen bir zorlama düşünce tarzı mıdır? Bu soruların yanıtını bilemesek de bilimsel veriler ışığında emin olacağımız tek şey evrenin ciddi bir matematik kuralına göre işlediğidir.
GÜNEŞ SİSTEMİ VE EVREN
İlginçtir ki güneş sistemi ve evrende bile Altın Oran’ı bulabiliyoruz. Dünya ve Ay’ın çapları, boyutları Fi’nin matematiksel özelliklerine dayanan bir üçgen oluşturur. Gezegenlerin güneşten uzaklıkları, Fi’nin üstel güçleriyle şaşırtıcı bir şekilde yakından ilişkilidir. Satürn’ün güzel halkaları, boyut olarak gezegenin çapının Altın Oranı’na çok yakındır. NASA, 2003 yılında Evren’in şeklinin Fi’ye dayalı bir dodekahedron (on iki adet yüzü olan üç boyutlu şekil) olduğu bulgularını yayımlamıştır.
SANAT, MİMARLIK VE TASARIM
Altın Oran’ın tüm benzersiz matematiksel özellikleri ve yaratılıştaki görünümü ile insanlığın sadece bu sayıyı ve sihrini fark etmekle kalmayıp aynı zamanda kendi üretimiyle de doğanın güzelliğini ve uyumunu yakalamak için sanat, mimari ve tasarımın diğer alanlarında kullanması şaşırtıcı değildir. Bazı durumlarda, insanlığın Fi uygulaması
yadsınamaz. Mısır Büyük Piramidi’nin taban, yükseklik ve hipotenüs oranları Altın Oran’ı
temsil ediyor gibi görünüyor. Buna karşın eksik dış kabuğu ve eski Mısır yazılarında
Fi’den bahsedilmemesi, piramidin Altın Oran tasarımına uygun olduğunu kesin olarak
kanıtlamayı zorlaştırıyor.
Yunanlılar, Partenon’un inşası sırasında Fi’yi biliyordu ve genel boyutları Altın Oran’a
yaklaşırken sütunların üzerindeki kirişin tasarımında kullanıldığına dair kanıtlar var gibi görünüyor. Leonardo Da Vinci’nin 1500’lü yıllarda “İlahi Oran” olarak bilinen Fi’yi birçok resminde kullandığı bilinmektedir. Matematik, geometri, tıp gibi birçok bilime olan yatkınlığını sanatına yansıtan bu dâhinin Altın Oran’ın büyüsüne kapılmaması imkânsızdı zaten.
“Vitruvius Adamı” adı verilen çizimin “ideal insan” olarak tanımlanmasının bir nedeni
de bütün uzuvlarının açılarının oranının Altın Oran olması olabilir mi? “Mona Lisa”, “Son Akşam Yemeği”, “Aziz Jerome” gibi eserleri Altın Oran şemasına uygun olarak çizilmiştir. Bu dünyaca ünlü tabloların boyunun enine oranı tartışmasız olarak Altın Oran’dır. Michelangelo, Picasso, Salvador Dali, Raphaello Sanzio, Sandro Botticelli ve Georges Seurat gibi ünlü isimler de tablolarında Altın Oran’ı çokça kullanmıştır. Altın Oran’ın mimaride daha modern
uygulamaları Paris’te Notre Dame’de, New York’ta Birleşmiş Milletler Genel Merkez
Sekreterliği binasında ve Toronto’da CN Kulesi’nde görülebilir.
Ürünlerin ve logoların tasarımında birçok büyük şirket tarafından yaygın olarak
kullanılmaktadır. 2004’te duyurulan Vogue, Elle ve Vanity Fair tarafından kapsanan “Fi Koleksiyonu” gibi yüksek moda giyim tasarımında bile kullanılmıştır. Aynı zamanda kadın giyimine yönelik bir stil rehberi olan The Fashion Code’un da temelidir. Altın bir dikdörtgenin, insan gözünü en çok memnun eden dikdörtgen olup olmadığını görmek için
çeşitli çalışmalar test edilmiştir. Çalışmaların sonuçları karışıktır ancak genellikle sevindirici
olarak altın dikdörtgene yakın şekillere sahip dikdörtgenlere işaret etmektedir. Mimar Sinan’ın birçok eserinde Altın Oran karşımıza çıkmaktadır. Süleymaniye ve Selimiye Camilerinin ihtişamında Altın Oran’ın payını da azımsayamayız.
MÜZİK
Müzik ve akustikte de Altın Oran rol oynar. Yapılan araştırmalar, Mozart’ın yazdığı 18 piyano eserinden altı tanesinin tam anlamıyla altın orana uyduğunu, sekiz tanesinin ise bu orana çok yakın olduğunu ortaya koymuştur.
TIP
Akciğerlerde Altın Oran: 1985 ve 1987 yılları arasında yapılan bir çalışmada, Dr. A. L.
Goldberger ve arkadaşları makalelerinde, akciğerin yapısında Altın Oran’ın varlığını
ortaya koymuştur. Akciğeri oluşturan bronş ağının bir özelliği de asimetrik olmasıdır.
Örneğin, nefes borusu biri uzun (sol) ve diğeri kısa (sağ) olmak üzere iki ana bronşa
ayrılır. Bu asimetrik bölünme, bronşların sonraki alt bölümlerine doğru devam eder.
Tüm bu bölünmelerde kısa bronşun uzun bronşa oranının her zaman 1.618 olduğu
belirlenmiştir.
Kalpte ve DNA’da Altın Oran: Kalp performansının Altın Oran yasasına tabi olduğundan şüphelenilebilir. Bu hipotez, Rus Biyolog Zvetkov tarafından gerçekleştirilen memelilerin kalp ritmi ile ilgili araştırmaların temelini oluşturmaktadır. Kardiyogramda sistolik (t1) ve diyastolik (t2) kalp aktivitesine karşılık gelen farklı sürelerde iki uzunluk seçilebilir. Zvetkov, insan ve diğer memeliler için optimal (“altın”) çarpıntı frekansının var olduğunu tespit etmiştir. Bir diğer ifadeyle burada sistol, diyastol ve tam kalp döngüsü ( T) sürelerinin T:t1=t2:t1 oranın Altın Oran olduğunu göstermiştir.
Tüm yaşamın formülünü taşıyan DNA molekülü, yaşamın programını taşımakta ve her tam turunda, 34 angström uzunluğunda ve 21 angström genişliğindeki çift spiral yapısında bulunmaktad
 ır. 21 ve 34 sayılarının birbirine oranı 1,6190476 olup yaklaşık olarak 1,6180339 Altın Oran’ı vermektedir.
ır. 21 ve 34 sayılarının birbirine oranı 1,6190476 olup yaklaşık olarak 1,6180339 Altın Oran’ı vermektedir.
GÜZELLİK ALGILARI
(YÜZ VE DİŞ ESTETİĞİ)
Yüzümüzde Altın Oran’ı görebileceğimiz birçok yer vardır, örneğin kaşların arasındaki boşluk ile gözbebekleri arasındaki boşluğun oranı; ağzımızdaki ön iki dişin enlerinin boylarına oranı; ağız uzunluğu ile burun genişliğinin oranı, burun genişliği ile burun delikleri arasındaki uzaklığın oranı; yüz boyu ile yüz genişliğinin oranı; alt dudak genişliği ile üst dudak genişliğinin oranı birer Altın Oran’dır. Bilim adamları ve sanatçılar tarafından belirlenen bu “ideal insan yüzü” tanımına her yüzün uyması beklenemez ancak Marilyn Monroe, Alessandra Ambrosio, Katy Perry, Kelly Brook, Jessica Alba, Rita Ora, Kate Moss, Helen Mirre, Scarlett Johansson, Salma Hayek, Amber Heard (Altın Oran’a en yakın yüz) gibi ünlü isimlerin yüzleri Altın Oran’a oldukça yakındır.

İnsan vücudunun bir parçası olan kollar; dirsek, alt ve üst bölüm olmak üzere iki bölüme ayırır. Kollarımızın üstündeki bölgenin alt bölüme oranı ve kolların tamamının üst bölüme oranı Altın Oran’dır. Parmaklarınızın üst boğumunun altındaki boğuma oranı ve tamamının üst boğumuna oranı yine Altın Oran’ı vermektedir. Plastik ve Rekonstrüktif Cerrahi Uzmanı
Prof. Dr. Onur Erol, “Altın Oran’ı oluşturmak için neler yapılabilir?” sorusuna yanıt olarak
burun, alın, kaşlar, yanaklar, dudaklar, çene ve kulaklar için uygulanacak Altın Oran’a sahip bir yüzümüzün nasıl olacağını açıklamıştır.
Doğadan varlığını keşfettiğimiz ve matematik bir modele uydurduğumuz bir olgu olan Altın
Oran, gerçekten güzelliğin sırrı mı yoksa göz alışkanlığından gelen bir kabul mü? Bu soru tartışılır. Fi’nin insan formunda yüz, vücut, parmaklar, dişler hatta DNA’mızdaki kapsamlı görünümü ve bunun insan güzelliği algılarımız üzerindeki etkisi daha da ilgi çekicidir. Bazıları güzelliğin bakanın gözünde olduğunu iddia edebilir ancak kadınlarda ve erkeklerde güzellik olarak algıladığımız şeyin yüz ve vücut boyutlarının oranlarının Fi’ye ne kadar yakın olduğuna bağlı olduğunu destekleyen kanıtlar vardır. Bu nedenle hem yüz plastik cerrahisinde hem de estetik diş hekimliğinde Fi yüz hatlarında ve görünümünde en doğal ve güzel sonuçlara ulaşmak için bir rehber olarak uygulanmaktadır.

İlk olarak Dr. Arthur Swift ve Dr. Kent Remington tarafından kavramsallaştırılan BeautPHIcation™; genç yüz konturunu, şeklini ve hacmini geri kazandırmak için daha kapsamlı bir yaklaşım elde üzere tasarlanmış bir yüz dolgu prosedürüdür. Leonardo Da
Vinci’nin Mona Lisa ve Vitruvius Adamı gibi eserlerde güzellik ve uyum yaratmak için kullandığı aynı matematiksel ilkelere dayanmaktadır. Türkiye’den birçok cerrah Kanada’da “The Phi Adamı” olarak isimlendirilen Dr. Arthur Swift‘in botox, dolgu ve yüz şekillendirmede Altın Oran ile ilgili seminerlerine katılmıştır.
Plastik ve Rekonstrüktif Cerrahi Uzmanı Prof. Dr. Orhan Babuçcu ve Opr. Dr. Berfu Babucçu’nun, “Benim yüzüm neden Altın Oran değil?’ diye üzülmeyin çünkü yüz estetiği uygulamaları ile Altın Oran olmak ya da Altın Oran’ı yakalamak mümkündür. Altın Oran’lı yüzler, çoğunlukla herkes tarafından estetik, güzel, çekici olarak kabul edilir ancak Altın Oran’lı yüzler de zamanla yüzündeki Altın Oran’ı kaybedebilir. Yaşlanma, stres, yanlış
beslenme, hareketsizlik gibi tüm faktörler ideal yüz formunu bozabilecek faktörlerdir. Bu durumda da Altın Oran yüz estetiği işlemleri yani profiloplasti ile Altın Oran ideal yüz orantısını yakalama şansı vardır.” şeklindeki değerlendirmesi bir diğer ifadeyle güzellik ve Altın Oran’ın beraber anıldığını vurgulaması bir matematikçi olarak hoşuma gitmedi değil.
Diş estetiği üzerine yapılan The Golden Proportion çalışmasında, Altın Oran’ın, diş dizilimi teşhisinde ve estetik diş tedavisi uygulamasında simetri, baskınlık ve oranın değerlendirilmesinde faydalı bir araç olduğu öne sürülmüştür. “Altın Oran, bir diş cerrahının bilmesi gereken bir tasarım unsurudur. Uzun zamandır güzelliği temsil eden bu esrarengiz oranın anlaşılması, bize mevcut bilgilerimizle birleştirilebilecek ve diş estetiğini makul
bir başarı güvencesi ile restore etmek için dişçilik çalışmalarımıza uygulanabilecek faydalı kılavuzlar sağlayabilir.” denilerek artık diş estetiğinde de altın oranın yer aldığı vurgulanmıştır. “Esthetic Dentistry and the Golden Proportion adlı çalışmada da, “…Tartışmalı olmasına rağmen Altın Oran, maksiller dişlerin düzeninin önden görünümündeki oranları değerlendirmek için matematiksel bir araç olarak savunulmaktadır. Estetik, güzellik çalışmasını ve ona verilen duygusal tepkileri kapsar. Estetik diş tedavisi, güzellik yanılsaması yaratmak için tasarlanmış sanatsal ve öznel bileşenleri içerir. Bu nedenle estetik ilkelerin daha iyi anlaşılması gerekmektedir. Güzel gülümsemelerin bilimsel analizi, diş estetiğini tahmin edilebilir şekillerde değerlendirmek ve geliştirmek için Altın Oran ilkesinin sistematik olarak uygulanabileceğini göstermiştir.” vurgusu yapılmıştır.
MANEVİ YÖNLER
Altın Oran’ın, birçok kişi tarafından yaşamdaki güzellik ve maneviyat hakkında daha derin bir anlayışa açılan bir kapı olarak görülmesi ve gördüğümüz pek çok şeyde gizli bir uyum veya bağlantılılık ortaya çıkarması nedeniyle İlahi Oran olarak da tanımlanması belki de uygundur.
Bu tek sayı, insanlık tarihinde ve yaşamın temellerinde inanılmaz bir rol oynadı. Matematiksel ve gizemli yönleri arasındaki çizgi bu nedenle kolayca çizilmez. Fi, İncil’de veya diğer eski kutsal metinlerde açıkça görülmez ancak Allah’ın gemi için Hz. Nuh Peygamber’e ve Ahit Sandığı için Hz. Musa Peygamber’e verdiği boyutların her ikisinin de 5’e 3 oranını (1,666) yansıttığını, Fibonacci sayılarının bir orana sahip olduğunu görüyoruz ki bu oran Fi’ye oldukça yakın bir yaklaşımı ifade eder. İslam’ın Mekke’deki en kutsal yeri olan Kâbe, Dünya’nın Kuzey ve Güney kutupları arasındaki mesafenin altın oranına çok yakın bir yerde bulunmaktadır. İlginçtir ki içinden bir çizgi çizilen bir daire olan Fi sembolü bile yaratıcının evreni yoktan yaratmasına benzer şekilde, güzelliği yaratmak için bir sıfırı,
boşluğu, bire bölünmüş boşluğu veya birliği temsil ettiği düşünülebilir.
Akıl meselelerinde görmek inanmaktır ama iman meselelerinde ilk önce görmenin kapısını açan inanmaktır. Görme algımıza derinlik katmak için iki göze ihtiyacımız olduğu gibi hem inanç hem de akıl, yaşam ve içinde yaşadığımız evren anlayışımıza derinlik katmamıza hizmet etmektedir. Kısaca, altın oranın doğadaki görünüşlerinin yaratıcının yaratma sıfatının muazzamlığının bir ispatı olduğunu söyleyebiliriz.
ALTIN ORAN İLE İLGİLİ YENİ
KEŞİFLER
Altın Oran, yaşam ve evren anlayışımızda yeni kapılar açmaya devam etmektedir. Roger
Penrose’un 1970’lerde, daha önce imkânsız olduğu düşünülen bir görev olan, yüzeylerin
beş katlı simetride döşenmesine izin veren “Penrose Fayansları” keşfinde Altın Oran ortaya
çıkmıştır. 1980’lerde yeni keşfedilen bir madde formu olan yarı kristallerin üç boyutlu
moleküler düzenlemesinde tekrar altın oran sihrini göstermiştir.
21. yüzyılda Fi, zaman ve kuantum fiziği de dâhil olmak üzere çok çeşitli çalışma alanlarında yeniden doğuyor gibi görünüyor. Tüm bunlara ilaveten ülkemizde anatomi,
diş hekimliği, müzik, metalurji mühendisliği, biyoistatistik, bilgisayar mühendisliği,
mimarlık ve güzel sanatlar alanlarında Altın Oran’ın büyüsüne kapılıp lisansüstü tezler de
yapılmaktadır.
Eminim ki bundan sonra da bu büyüyü çözmeye çalışan birçok tez, araştırma yapılacak ve ilahi sihir cazibesini koruyacaktır.
En derin saygılarımla.

 yüzyıl astronomu ve 21. yüzyıl romancısının hakkında çalışmalar yapacak kadar ilginç yapan nedir? Kısaca açıklamaya çalışayım: Yunanca Fi harfi ile temsil edilen bu ‘‘altın’’ sayı, 1.61803399…olup birçok isimle anılır. Altın Oran, Altın Sayı, Altın Ortalama, Altın Bölüm, İlahi Oran ve İlahi Bölüm olarak bilinir. Hayatın pek çok yönü için geçerli olan tasarım sabiti diyebileceğimiz Fi, alışılmadık bir şekilde sık sık ortaya çıkan
yüzyıl astronomu ve 21. yüzyıl romancısının hakkında çalışmalar yapacak kadar ilginç yapan nedir? Kısaca açıklamaya çalışayım: Yunanca Fi harfi ile temsil edilen bu ‘‘altın’’ sayı, 1.61803399…olup birçok isimle anılır. Altın Oran, Altın Sayı, Altın Ortalama, Altın Bölüm, İlahi Oran ve İlahi Bölüm olarak bilinir. Hayatın pek çok yönü için geçerli olan tasarım sabiti diyebileceğimiz Fi, alışılmadık bir şekilde sık sık ortaya çıkan
 oluşturan sayılar Fibonacci sayıları, Fn olarak bilinir. Fibonacci dizisinin Altın Oran ile olan ilişkisi, her sayının kendisinden öncekine bölünmesiyle bulunur. Dizide ne kadar ileri gidilirse sonuç Fi’ye o kadar yakın olur.
oluşturan sayılar Fibonacci sayıları, Fn olarak bilinir. Fibonacci dizisinin Altın Oran ile olan ilişkisi, her sayının kendisinden öncekine bölünmesiyle bulunur. Dizide ne kadar ileri gidilirse sonuç Fi’ye o kadar yakın olur.
 e karelerin karşılıklı köşelerini Fibonacci sayılarıyla birleştiren yaylar çizilerek sarmal oluşturulabilir ve bu köşegenlerin kesişme noktası logaritmik sarmalın başlangıç noktasını verir.
e karelerin karşılıklı köşelerini Fibonacci sayılarıyla birleştiren yaylar çizilerek sarmal oluşturulabilir ve bu köşegenlerin kesişme noktası logaritmik sarmalın başlangıç noktasını verir.

 ır. 21 ve 34 sayılarının birbirine oranı 1,6190476 olup yaklaşık olarak 1,6180339 Altın Oran’ı vermektedir.
ır. 21 ve 34 sayılarının birbirine oranı 1,6190476 olup yaklaşık olarak 1,6180339 Altın Oran’ı vermektedir.


