Karmaşık yapıya sahip problemlerin çözümünde önemli bir yer tutmasından dolayı bilgisayar ile yapılan modellemelerin birçoğunda graph teorisinden faydalanıldığını biliyoruz.
Genel olarak bu teorinin temel amacı, iki nokta arasındaki güzergahı veya bağlantıları ortaya çıkarmak. Graph teorisinin doğum tarihini, İsviçreli matematikçi Leonhard Euler’in Königsberg’in yedi köprüsü (Orj: Die Sieben Brücken von Königsberg) problemi ile ilgili yazdığı makalenin tarihi olan 1736 yılı olarak kabul edebiliriz. Peki günümüzde hala popülerliğini koruyan bu problem nasıl ortaya çıktı?
Her şey aslında Königsberg kentinde ortaya atılan bir sorunun yayılarak Euler’in kulağına gitmesiyle başladı. Şehirde Eski ve Yeni Pregel nehirleri birleşerek Pregel (Pregolya) nehrini oluşturuyordu. Bu nehirler şehri dört bölüme ayırıyordu ve bu dört bölümü birleştiren yedi köprü bulunmaktaydı (ancak köprülerin ikisi II. Dünya Savaşı sırasında bombardımanlarla yok edilirken kalan iki tanesi de Ruslar tarafından yıkılmıştır). Bu köprülerle ilgili bir sorunun halk arasında kulaktan kulağa yayılarak sınırları aşmasıyla Königsberg’in yedi köprüsü problemi de doğmuş oldu: Bütün köprülerden yalnız bir defa geçmek koşulu ile bir yürüyüş yapılabilir mi?
Bu soruyu biraz daha detaylandıracak olursak, “her köprüden sadece bir kez geçmek koşuluyla tüm şehir dolaşılabilir mi?” sorusu halkı çokça cezbetti, ancak birçok defa denense de kimse olumlu bir sonuç elde edemedi. Sınırları aşan bu teori en sonunda Euler’in de kulağına gitti ve bir matematikçi olan Euler, şehri gezmek yerine problemin çözümünü kâğıt üzerinde aramaya başladı. Euler, bir matematikçiye yakışacak şekilde şehrin krokisini çizmek yerine aşağıdaki gibi bir graph modeli üzerinden problemi çözmeye çalıştı – ki bu çizime ilk graph modeli diyebiliriz. Ancak Euler bu çizimle çözümü bulabildi mi? Hayır, ancak problemin yanlışlığını kanıtlamış oldu. Peki bu soruna çözümü ne oldu?
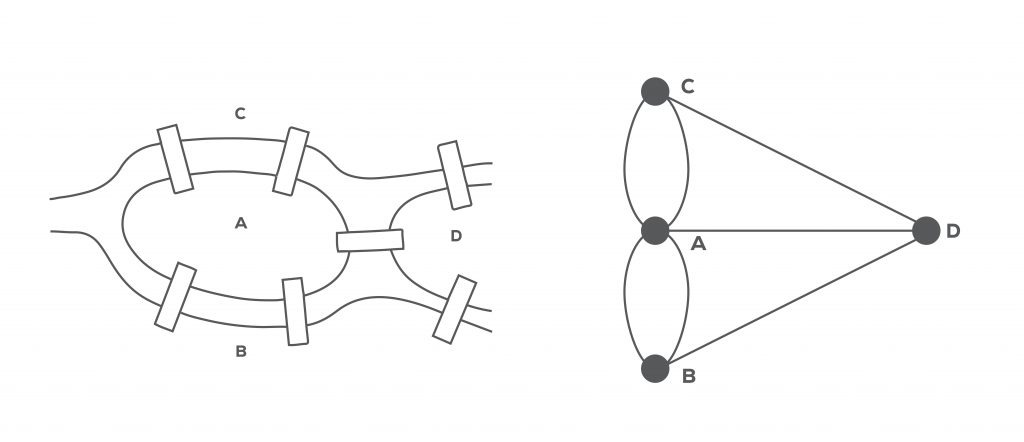
Çözümü sizlere anlatmadan önce graph modelinin temel elemanları nodge, edge ve graph derecesi kavramlarını tekrar hatırlayalım * . Bu çizimde kara parçaları node’ları oluştururken, köprüler edge’leri oluşturuyor ve her bir node’dan çıkan edge sayısı da düğümün derecesini tanımlıyor. İşte Euler bu çizimle, bütün köprüleri birer defa kullanarak tüm bölgeleri ziyaret edebilmek için tek dereceli düğümlerin iki tane olması -ki bu düğümler başlangıç ve bitiş noktalarını gösteriyor- diğer düğüm derecelerinin de çift olması gerektiğini ortaya koydu – ki çıkış ve dönüş yolları eşit olsun. Eğer başlangıç ve bitiş noktalarının aynı olması isteniyorsa, tüm düğüm derecelerinin çift olması gerekiyordu. Bu graph modeline göre yukarıdaki koşullar sağlandığında tüm köprülerden bir kez geçerek problemimizin çözümüne ulaşabiliyoruz.
İşte bu problem ve Euler’in çizimiyle graph teorisinin temelleri atılmış oldu. Çözümün ardından Euler, “Solutio problematis ad geometriam situs pertinentis” isimli makaleyi yayınladı.
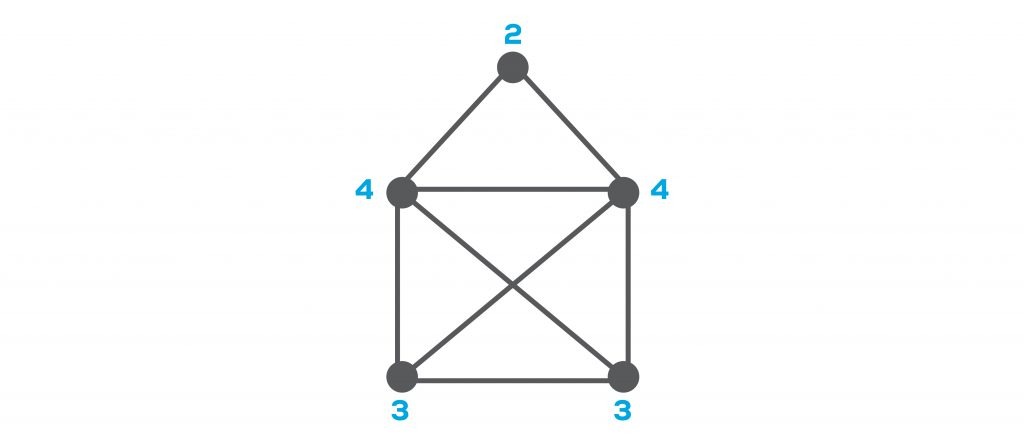
Graph mantığı üzerine kurulu problemlerle günlük hayatımızda aslında sıkça karşılaşıyoruz. Örneğin aşağıdaki görselde en çok denk geldiklerimizden bir tanesi mevcut. Buradaki soruya mutlaka bir kez denk gelmişsinizdir; çizim üzerinde çizgilerden yalnızca bir kez geçerek, yani elimizi kaldırmadan, çizimi tamamlayabilir miyiz? Bunu da aslında bir graph problemi olarak tanımlayabiliriz ve görebileceğimiz gibi tek dereceli düğümlerden başlarsak tüm çizgilerden bir kez geçerek çizimi tamamlayabiliyoruz. Görsel üzerinden deneyebilirsiniz 🙂
İki varlık arasındaki en kısa yolu bulma (shortest path) gibi graph algoritmalarını günlük hayatımızın her alanında kullanıyoruz * . Verilerin analizi ve veriler arasındaki bağlantı ve ilişkilerin ortaya çıkarılmasında kullandığımız graph temelli algoritmaların temeli de işte Königsberg’in yedi köprüsü problemi ile ortaya çıkmış oluyor.