We know that graph theory is used in most computer modeling since its importance in solving problems with complex structures.
Generally, the main purpose of this theory is to reveal the paths or connections between two points. We can accept the birth date of graph theory as the year 1736, which is the date of the Swiss mathematician Leonhard Euler’s article on the seven bridges of Königsberg (Original: Die Sieben Brücken von Königsberg). So how did this problem, which is still popular today, emerge?
Everything actually begun when a problem arose in the city of Königsberg reached Euler’s ears. The Old and New Pregel rivers merged in the city to form the Pregel (Pregolya) river. These rivers divided the city into four lands, and there were seven bridges connecting these four lands (although two of the bridges were destroyed by bombardment during World War II, while the remaining two were destroyed by the Russians). The problem of the seven bridges of Königsberg arose when a problem related to these bridges spread among the people by word of mouth: Is it possible to walk around the city by crossing all bridges only once?
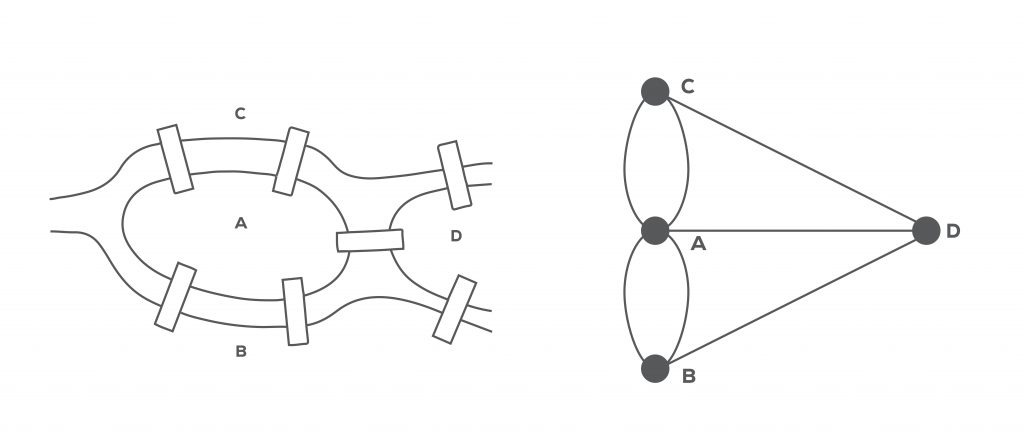
Let’s elaborate on this question a little more, “Can the whole city be visited by passing through each bridge only once?” attracted the public a lot, but even though it has been tried many times, no one has achieved a positive result. This cross-boundary theory eventually reached Euler, and he, as a mathematician, began to look for the solution of the problem on paper instead of visiting the city. Instead of drawing a map of the city, Euler tried to solve the problem by using a graph model like the one below – which we can assume as the first graph model. But did Euler find the solution with this drawing? No, but he proved that the problem is wrong. So, what is the solution to this problem according to Euler?

Before explaining the solution, let’s remember the basic elements of a graph model, which are nodes, edges, and graph degree concepts * . In this drawing, land pieces are nodes, bridges are edges, and the number of edges from each node defines the degree of the node. With this drawing, Euler demonstrated that to be able to visit all regions by using all bridges once, there must be two nodes of odd degree – which are the starting and ending points – and the other node degrees must be even – so that the exit and return paths are equal. If the starting and ending points should be the same, all node degrees had to be even. According to this graph model, when the above conditions are met, we can solve our problem by crossing all bridges once.
With this problem and Euler’s drawing, graph theory emerged. After the solution, Euler published the article “Solutio problematis ad geometriam situs pertinentis”.
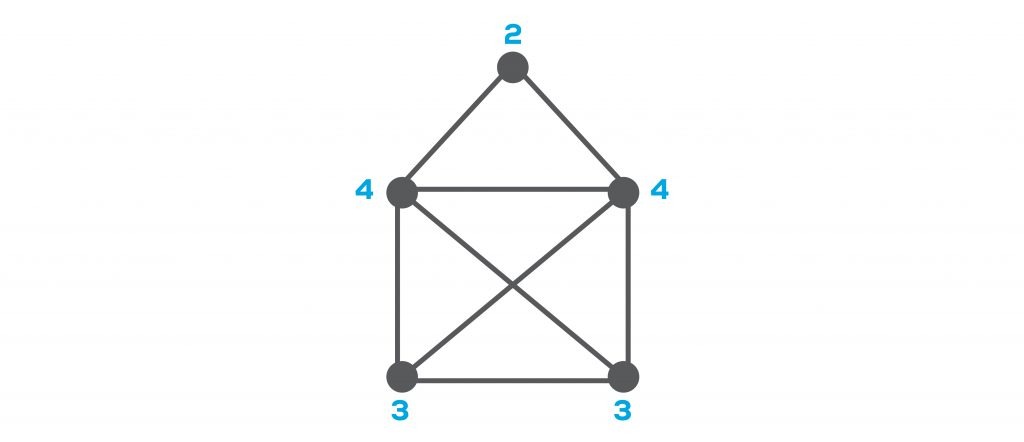
We often encounter problems based on graph logic in our daily lives. For example, the image below is one of the most common ones. You must have come across the question here once in your life; Can we complete the drawing by crossing the lines only once on the drawing without raising our hand? We can actually define this as a graph problem, and as we can see, if we start from nodes of odd degree, we can complete the drawing by passing through all the lines once. Let’s try on the picture below ?
We use graph algorithms such as the shortest path between two entities in many areas of our daily life * . The basis of the graph-based algorithms we use in analyzing and revealing the connections and relationships between data is revealed with the problem of Königsberg’s seven bridges.